凸轮计算需要输入的数据
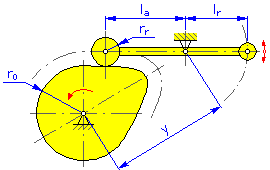
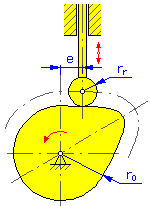
- 基本半径 r 0 (盘式凸轮和圆柱凸轮)
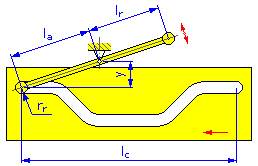
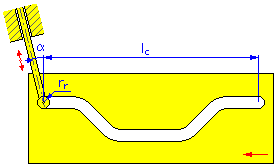
- 运动长度 l c (线性凸轮)
- 凸轮宽度 b c
- 滚子半径 r r
- 滚子宽度 b r (对于从动件形状圆柱)
- 偏心 e(用于平动从动件的盘式凸轮)
- 偏心角 α(用于平动从动件的线性凸轮和圆柱凸轮)
- 枢轴距离 y(用于摆动臂的盘式凸轮和线性凸轮)
- 臂长度 l a (用于摆动臂的盘式凸轮和线性凸轮)
- 反作用力臂 l r (用于摆动臂的盘式凸轮和线性凸轮)
- 速度 ω(盘式凸轮和圆柱凸轮)
- 速度 v(线性凸轮)
- 滚子上的力 F
- 加速的重力 m
- 弹性率 c
- 许用压力 p A1
- 凸轮材料的弹性模量 E 1
- 凸轮材料的泊松比 μ 1
- 许用压力 p A2
- 从动件材料的弹性模量 E 2
- 从动件材料的泊松比 μ 2
| 盘式凸轮 | |
 |  |
| 线性凸轮 | |
 |  |
| 圆柱凸轮 | |
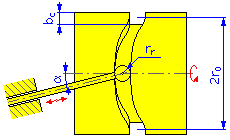 | |
| 外径 = 2r 0 + b c | |
| 内径 = 2r 0 – b c | |
凸轮段
- 运动函数 f y (z) [ul]
- 倒转比 k r (仅用于“抛物线”和“具有线性部分的抛物线”运动)
- 线性部分 k l (仅用于“具有线性部分的抛物线”运动)
- 运动起始位置 l 0 [°; mm, in]
- 运动终止位置 l [°; mm, in]
- 段运动长度 dl = l – l 0 [°; mm, in]
- 起始行程 h 0 [mm, in]
- 结束行程 h max [mm, in]
- 段行程 d h = h max – h 0 [mm, in]
行程从属性
盘式凸轮和圆柱凸轮
凸轮旋转角 ϕ i [°]
在段中的实际相对位置:z i = (ϕ i – l 0 )/dl(范围 0 – 1)
| 行程 | y i = dh f y (z) [mm, in] |
| 速度 | |
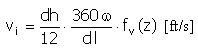 | |
| 加速度 | 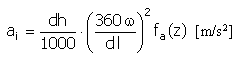 |
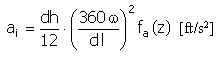 | |
| 跃度 | 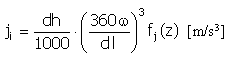 |
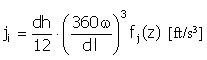 |
线性凸轮
凸轮运动位置 l i [mm, in]
在段中的实际相对位置:z i = (l i – l 0 )/dl(范围 0 – 1)
| 行程 | y i = dh f y (z) [mm, in] |
| 速度 | |
| 加速度 | 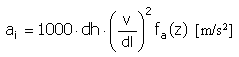 |
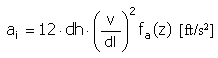 | |
| 跃度 | 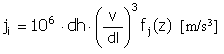 |
 |
凸轮运动函数
摆线(延长的正弦曲线)
此运动具有出色的加速特性。此运动通常用于高速凸轮,因为它可以实现低级别噪音、振动和磨损。
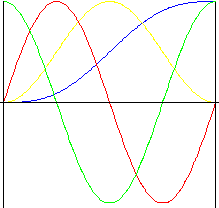
| 行程 | |
| 速度 | |
| 加速度 | |
| 跃度 |
| 行程 | f y (z) = z – 0.5/π sin(2πz) |
| 速度 | f v (z) = 1 – cos (2πz) |
| 加速度 | f a (z) = 2π sin(2πz) |
| 跃度 | f j (z) = 4π 2 cos(2πz) |
谐波(正弦曲线)
在冲击期间可以保持平滑的速度和加速度是该曲线的固有优势。但是,在运动起点和终点处,加速度的瞬间变化会导致振动、噪音和磨损。
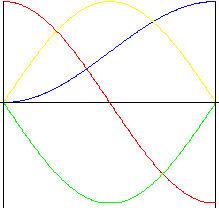
| 行程 | |
| 速度 | |
| 加速度 | |
| 跃度 |
| 行程 | f y (z) = 0.5 (1 – cos πz)) |
| 速度 | f v (z) = 0.5 π sin (πz) |
| 加速度 | f a (z) = 0.5 π 2 cos(πz) |
| 跃度 | f j (z) = -0.5π 3 sin(πz) |
线性
在运动起点和终点处会产生巨大冲击的简单运动。很少使用这种运动(除非在非常简易的设备中)。建议您使用已修改运动起点和终点的运动 – 具有线性部分的抛物线。
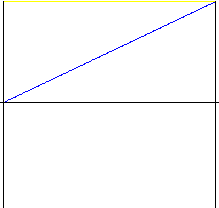
| 行程 | |
| 速度 |
| 行程 | f y (z) = z |
| 速度 | f v (z) = 1 |
| 加速度 | f a (z) = 0 |
| 注: z = 0 和 z = 1 时,正确值应该是无穷大的值,但计算时不能使用无穷大的值,要使用零。 | |
| 跃度 | f j (z) = 0 |
| 注: z = 0 和 z = 1 时,正确值应该是无穷大的值,但计算时不能使用无穷大的值,要使用零。 |
抛物线(2 nd 阶多项式)
具有最小可能加速度的运动。但是,若在运动的起点、中间和终点处加速度突然变化,也会产生冲击。倒转比使得可以通过运动中的“拉伸”来允许加速度和加速度比率的变化。
对称(倒转比 k r = 0.5)

| 行程 | |
| 速度 | |
| 加速度 |
| z = 0 至 0.5 时: | |||
| 行程 | fy(z) = 2z 2 | ||
| 速度 | fv(z) = 4z | ||
| 加速度 | fa (z) = 4 | ||
| 跃度 | fa(z) = 0 | ||
| z = 0.5 至 1 时: | |||
| 行程 | fy(z) = 1 – 2(1 – z) 2 | ||
| 速度 | fv(z) = 4 (1 – z) | ||
| 加速度 | fa (z) = -4 | ||
| 跃度 | fj(z) = 0 | ||
| 注: z = 0 和 z = 1 时,正确值应该是无穷大的值,但计算时不能使用无穷大的值,要使用零。 | |||
非对称
k r – 倒转比(在范围 0.01 至 0.99 内)
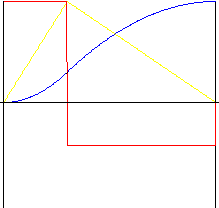
| 行程 | |
| 速度 | |
| 加速度 |
| z = 0 至 k r 时: | |||
| 行程 | f y (z) = z 2 / k r | ||
| 速度 | f v (z) = 2z / k r | ||
| 加速度 | f a (z) = 2 / k r | ||
| 跃度 | f j (z) = 0 | ||
| z = k r 至 1 时: | |||
| 行程 | f y (z) = 1 – (1 – z) 2 / (1 – k r ) | ||
| 速度 | f v (z) = 2 (1 – z) / (1 – k r ) | ||
| 加速度 | f a (z) = -2 / (1 – k r ) | ||
| 跃度 | f j (z) = 0 | ||
| 注: z = 0 和 z = 1 时,正确值应该是无穷大的值,但计算时不能使用无穷大的值,要使用零。 | |||
具有线性部分的抛物线
可以比线性运动提供更多合适的加速度和减速度。倒转比使得可以通过运动中的“拉伸”来允许加速度和加速度比率的变化。线性零件比允许设置线性运动零件的相对大小。

| 速度 | |
| 加速度 | |
| 跃度 |
k r – 倒转比(在范围 0.01 至 0.99 内)
k l – 线性部分比(在范围 0 至 0.99 内)
k z = 1 + k l / (1 – k l )
k h = (1 – k l ) / (1 + k l )
| z = 0 至 k r / k z 时: | |||
| 行程 | f y (z) = k h z 2 k z 2 / k r | ||
| 速度 | f v (z) = 2 k h z k z 2 / k r | ||
| 加速度 | f a (z) = 2 k h k z 2 / k r | ||
| 跃度 | f j (z) = 0 | ||
| z = k r / k z 至 r / k z + k l 时: | |||
| 行程 | f y (z) = (z – 0.5 k r / k z ) 2 / (1 + k l ) | ||
| 速度 | f v (z) = 2 / (1 + k l ) | ||
| 加速度 | f a (z) = 0 | ||
| 跃度 | f j (z) = 0 | ||
| z = k r / k z + k l 至 1 时: | |||
| 行程 | f y (z) = 1 – k h (1 – z) 2 k z 2 / (1 – k r ) | ||
| 速度 | f v (z) = 2 k h (1 – z) k z 2 / (1 – k r ) | ||
| 加速度 | f a (z) = -2 k h k z 2 / (1 – k r ) | ||
| 跃度 | f j (z) = 0 | ||
3 rd 阶多项式(3 次抛物线)
比 2 次抛物线运动所受冲击更小的运动。
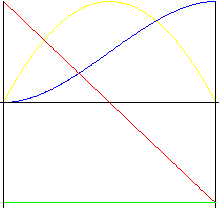
| 行程 | |
| 速度 | |
| 加速度 | |
| 跃度 |
| 行程 | f y (z) = (3 -2z) z 2 |
| 速度 | f v (z) = (6 – 6z) z |
| 加速度 | f a (z) = 6 – 12z |
| 跃度 | f j (z) = -12 |
4 th 阶多项式
比 3 rd 阶多项式运动所受冲击更小的运动。
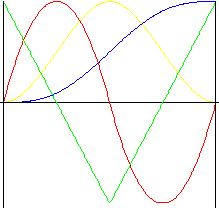
| 行程 | |
| 速度 | |
| 加速度 | |
| 跃度 |
| z = 0 – 0.5 时 | ||
| 行程 | f y (z) = (1 – z) 8z 3 | |
| 速度 | f v (z) = (24 – 32z) z 2 | |
| 加速度 | f a (z) = (48 – 96z) z | |
| 跃度 | f j (z) = 48 – 192z | |
| z = 0.5 – 1 时 | ||
| 行程 | f y (z) = 1 – 8z (1 – z) 3 | |
| 速度 | f v (z) = (32z – 8) (1 – z) 2 | |
| 加速度 | f a (z) = (48 – 96z) (1 – z) | |
| 跃度 | f j (z) = 194z – 144 | |
5 th 阶多项式
比 3 rd 阶多项式运动所受冲击更小的运动。
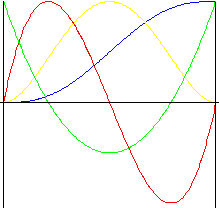
| 行程 | |
| 速度 | |
| 加速度 | |
| 跃度 |
| 行程 | f y (z) = (6z 2 – 15z + 10) z 3 |
| 速度 | f v (z) = (z 2 – 2z + 1) 30z 2 |
| 加速度 | f a (z) = (2z 2 – 3z + 1) 60z |
| 跃度 | f j (z) = (6z 2 – 6z + 1) 60 |
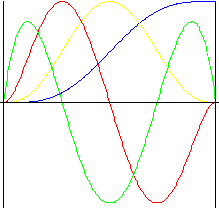
7 th 阶多项式
所有公式中的平滑度(包括跃度)
| 行程 | |
| 速度 | |
| 加速度 | |
| 跃度 |
| 行程 | f y (z) = (-20z 3 + 70z 2 – 84z + 35) z 4 |
| 速度 | f v (z) = (-z 3 + 3z 2 – 3z + 1) 140z 3 |
| 加速度 | f a (z) = (-2z 3 + 5z 2 – 4z + 1) 420z 2 |
| 跃度 | f j (z) = (-5z 3 + 10z 2 – 6z + 1) 840z |
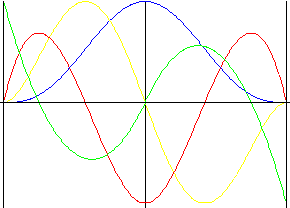
5 th 阶非对称多项式
与 5 阶多项式类似,但是具有强制返程。
注: 需要合并第 1 部分和第 2 部分。
| 行程 | |
| 速度 | |
| 加速度 | |
| 跃度 |
| 第 1 部分 | ||
| 行程 | f y (z) = 1 – (8 (1 – z) 3 – 15 (1 – z) 2 + 10) (1 – z) 2 / 3 | |
| 速度 | f v (z) = (2 (1 – z) 3 – 3 (1 – z) 2 + 1) (1 – z) 20 / 3 | |
| 加速度 | f a (z) = -(8 (1 – z) 3 – 9 (1 – z) 2 + 1) 20 / 3 | |
| 跃度 | f j (z) = (4 (1 – z) 2 – 3 (1 – z)) 40 | |
| 第 2 部分 | ||
| 行程 | f y (z) = (8z 3 – 15z 2 + 10) z 2 / 3 | |
| 速度 | f v (z) = (2z 3 – 3z 2 + 1) z 20/3 | |
| 加速度 | f a (z) = (8z 3 – 9z 2 + 1) 20/3 | |
| 跃度 | f j (z) = (4z 2 – 3z) 40 | |
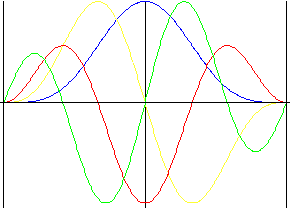
双谐
所有公式中的平滑度(包括跃度)都具有强制返程。
注: 需要合并第 1 部分和第 2 部分。
| 第 1 部分 | ||
| 行程 | f y (z) = cos(0.5π (1 – z)) 4 | |
| 速度 | f v (z) = π (0.5 sin(πz) – 0.25 sin(2πz)) | |
| 加速度 | f a (z) = 0.5 π 2 (cos(πz) – cos(2πz)) | |
| 跃度 | f j (z) = π 3 (-0.5 sin(πz) + sin(2πz)) | |
| 第 2 部分 | ||
| 行程 | f y (z) = 1 – cos(0.5π z) 4 | |
| 速度 | f v (z) = π (0.5 sin(πz) + 0.25 sin(2πz)) | |
| 加速度 | f a (z) = 0.5 π 2 (cos(πz) + cos(2πz)) | |
| 跃度 | f j (z) = -π 3 (0.5 sin(πz) + sin(2πz)) | |
最大相对值的比较
| 运动 | 速度 | 加速度 | 跃度 |
| 摆线(延长的正弦曲线) | 2 | 6.28 | 39.5 |
| 谐波(正弦曲线) | 1.57 | 4.93 | 15.5 |
| 线性 | 1 | ∞ | ∞ |
| 抛物线(2 nd 阶多项式) | 2 | 4 | ∞ |
| 3 rd 阶多项式 | 1.5 | 6 | 12 |
| 4 th 阶多项式 | 2 | 6 | 48 |
| 5 th 阶多项式 | 1.88 | 5.77 | 60 |
| 7 th 阶多项式 | 2.19 | 7.51 | 52.5 |
| 5 th 阶非对称多项式 | 1.73 | 6.67 | 40 |
| 双谐 | 2.04 | 9.87 | 42.4 |
其他从属性
滚子上的力
| F i = F + m a i + c y i [N, lb] |
法向力
| Fn i = F i / cos (γ i ) [N, lb] |
力矩
| T i = F i r i tan (γ i ) [Nmm, lb in] |
特定(赫兹)压力
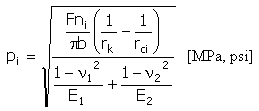 | |
| b = min (b v, b k ) |
